PDEs and the Schrödinger Equation

When learning calculus one starts with functions of a single variable and learns about derivatives of those functions categorized as differentiable. Once sufficiently understood, one can work with equations relating functions and their derivatives. Such equations are referred to as ordinary differential equations (ODEs). Later, functions of several variables are introduced and one learns of partial derivatives. A PDE, or partial differential equation, relates a function to its partial derivatives. For example, suppose $f$ is a function of two variables ( $x$ and $y$ ). Then

$\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2} = 0$

is a PDE known as the wave equation. The order of a PDE coincides with the highest order derivative that features in the equation. The wave equation above is a second order PDE.

PDEs are ubiquitous in physics. In quantum mechanics (QM) specifically it is a safe bet that the most famous equation is the Schrödinger Equation, which describes the evolution of state vectors for quantum systems. The time-dependent Schrödinger Equation is

$i\hbar \frac{\partial \psi}{\partial t} = \hat{H}\psi$

where $\hat{H}$ is called the Hamiltonian operator and usually corresponds to the total energy of the system. It is an example of what is known as a linear homogeneous PDE because it can be expressed in the form

$\mathcal{L}u = 0$

where $\mathcal{L}$ is a linear differential operator. We can see this by writing

$\left(i\hbar \frac{\partial}{\partial t} - \hat{H}\right)\psi = 0$

Solving the Schrödinger Equation is important because this part of QM is completely deterministic in that given the state of a system, say $\psi(x,0)$ , the Schrödinger Equation can be solved to determine the state of the system at any subsequent time.

When solving a linear PDE one should keep in mind something called the Superposition Principle:

If $u_1,..., u_n$ are solutions of the same linear homogeneous PDE $\mathcal{L}u = 0$ , and $c_1,..., c_n$ are constants (real or complex), then 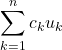$\displaystyle\sum_{k=1}^{n}c_k u_k$ is also a solution of the PDE.

Separation of Variables

A crucial technique for solving linear homogeneous PDEs is separation of variables. Suppose we have a PDE in $x$ and $t$ . The gist of the method is to entertain the assumption that a solution of the form $u(x,t): = \phi(x)\tau(t)$ exists, which is referred to as a product solution or separated solution. We look for such solutions and try to obtain ODEs for $\phi(x)$ and $\tau(t)$ that we can solve. If we can find such solutions, then the Superposition Principle allows us to construct more general solutions as sums of separated solutions. Let’s see how this method works in the context of the Schrödinger Equation.

To make things more manageable, let’s assume we are working with the simple case of a single particle of mass $m$ moving in one dimension. It turns out that the Hamiltonian for this scenario is

$\hat{H} = -\frac{\hbar^2}{2m}\cdot \frac{\partial^2}{\partial x^2}+V(x)$

With this, the Schrödinger Equation becomes

$i \hbar \frac{\partial \psi(x,t)}{\partial t} = -\frac{\hbar^2}{2m}\cdot \frac{\partial^2 \psi(x,t)}{\partial x^2} + V(x)\psi(x,t)$

Suppose a quantum system is prepared in a state $\displaystyle \psi(x,0) = \sum_{n}c_n\varphi_{n}(x)$ , where the $\varphi_{n}(x)$ are a basis of Eigenvectors of interest. We’d like to determine how this state will evolve according to the Schrödinger Equation. For the moment write the state at a later time $t$ as

$\psi(x,t) = \sum_{n}c_{n}\varphi_{n}(x,t)$

Plugging this in leads to a need to solve

$i\hbar \frac{\partial}{\partial t}\varphi_{n}(x,t) = -\frac{\hbar^2}{2m}\cdot \frac{\partial^2}{\partial x^2}\varphi_{n}(x,t)+V(x)\varphi_{n}(x,t)$

Now let $\varphi_{n}(x,t) = \phi_{n}(x)\tau_{n}(t)$ and substitute into the equation to get:

$i\hbar\phi_{n}(x)\frac{d}{dt}\tau_{n}(t) = -\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\phi_{n}(x)\tau_{n}(x)+V(x)\phi_{n}(x)\tau_{n}(t)$

Supposing $\phi_{n}(x)\tau_{n}(t)\neq 0$ , divide both sides to get

$i\hbar \frac{\frac{d}{dt}\tau_{n}(t)}{\tau_{n}(t)} = -\frac{\hbar^2}{2m}\cdot \frac{\frac{d^2}{dx^2}\phi_{n}(x)}{\phi_{n}(x)} + V(x)$

Notice that the left-hand-side is function of $t$ alone whereas the right-hand-side is a function of $x$ alone. And because $x$ and $t$ vary independently of one another, this equation can only be satisfied if both sides are the same constant, which we’ll label as $E_{n}$ (since it corresponds to an energy level). This leads to two important results.

First

$i\hbar \frac{\frac{d}{dt}\tau_{n}(t)}{\tau_{n}(t)} = E_{n}$

which implies

$\frac{d}{dt}\tau_{n}(t) = -\frac{i E_{n}}{\hbar}\tau_{n}(t)$

This is an ODE of which the relevant solutions are $\tau_{n}(t) = e^{-iE_{n}t/\hbar}$ .

Second, we have

$-\frac{\hbar^2}{2m}\cdot \frac{\frac{d^2}{dx^2}\phi_{n}(x)}{\phi_{n}(x)} + V(x)$

which implies that

$-\frac{\hbar^2}{2m}\cdot \frac{d^2}{dx^2}\phi_{n}(x)+V(x)\phi_{n}(x) = E_{n}\phi_{n}(x)$

or perhaps more informatively

$\left(-\frac{\hbar^2}{2m}\cdot \frac{d^2}{dx^2}+V(x)\right)\phi_{n}(x) = E_{n}\phi_{n}(x)$

This says that the $\phi_{n}$ are solutions to the time independent Schrödinger Equation (notice that there is no $t$ ). In other words, the $\phi_{n}$ are energy eigenstates (since they are eigenvectors of $\hat{H}$ ) corresponding to the energy eigenvalues $E_{n}$ .

If we can now express the initial state $\psi(x,0)$ as a superposition of the energy eigenstates, say $\displaystyle \sum_{n}a_{n}\phi_{n}(x)$ , then we can go on to build a full solution to the time dependent Schrödinger Equation and account for the time updating by using the Superposition Principle so that

$\psi(x,t) = \sum_{n}a_{n}\phi_{n}(x)e^{-iE_{n}t/\hbar}$

Let’s see this in practice by working with a common example.

Particle In A Box

Suppose we have a particle confined to a one-dimensional box of length $L$ . We can think of the situation as confining the particle to the interval $B: = [0,L]$ on the $x$ -axis. For this scenario the potential energy is defined by

$V(x): = \begin{cases}0, & x\in B\\ \infty, & x\in \overline{B}\end{cases}$

We will now try to find the eigenvectors and eigenvalues of the Hamiltonian operator. In other words, we need to solve the time-independent Schrödinger Equation

$\hat{H}\psi = E\psi$

which specifically becomes

$-\frac{\hbar^2}{2m}\cdot \frac{d^2}{dx^2}\psi(x) = E\psi(x), \qquad 0\leq x\leq L$

with the boundary conditions $\psi(0) = \psi(L) = 0$ . However, let’s rewrite this as

$\frac{d^2}{dx^2}\psi(x) = -\frac{2mE}{\hbar^2}\psi(x)$

which is a second order ODE where two obvious solutions are $e^{i\sqrt{2mE}x/\hbar}$ and $e^{-i\sqrt{2mE}x/\hbar}$ . By the Superposition Principle anything of the form

$c_{1}e^{i\sqrt{2mE}x/\hbar}+c_{2}e^{-i\sqrt{2mE}x/\hbar}$

will also be a solution.

Using the identity $e^{ikx} = \cos(kx)+i\sin(kx)$ , such solutions can also be expressed in the form

$A\cos\left(\frac{\sqrt{2mE}}{\hbar} x\right)+B\sin\left(\frac{\sqrt{2mE}}{\hbar} x\right)$

For this specific situation, however, the boundary condition $\psi(0) = 0$ requires that $A = 0$ meaning that we are only interested in solutions of the form

$\psi(x) = B\sin\left(\frac{\sqrt{2mE}}{\hbar} x\right)$

Next, it is also required that $\psi(L) = 0$ , but since we are not interested in trivial solutions, this means we need to examine

$\sin\left(\frac{\sqrt{2mE}}{\hbar} L\right) = 0$

This implies that $\displaystyle \frac{\sqrt{2mE}}{\hbar} L = n\pi$ . Solving for $E$ yields the possible energy eigenvalues:

$E_{n} = \frac{n^2 \pi^2 \hbar^2}{2mL^2}, \quad n\in \mathbb{N}$

Substituting this into the solution form for $\psi$ and simplifying yields

$\psi_{n}(x) = B\sin\left(\frac{n\pi}{L}x\right)$

To determine a suitable value for $B$ , it is required in QM that the $\psi_{n}$ be normalized (due to the connection to probability). This translates to the requirement